activity on vertex network

the definition in logic

摘抄自某EDU:

definition A directed graph in which the vertices represent tasks or activities and the edges represent precedence relations between tasks.

To be careful: 在AOV中是不能有cycles, 让一个activity的开始要以自身的结束为条件, 这显然是不合理的, 即: Directed Acyclic Graph

the definition in mathematics

这个definition本质上就是DAG的definition

definition A graph G = (V,E), V and E are two sets, each edge is represented by a ordered pairs <u,v> V: finite non-empty set of vertices E: set of pairs of vertices, edges

Example: a graph G

DAG

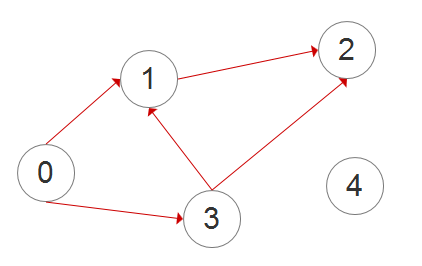
the realization in computer science

public class AOVNetwork {
    private int V;//no and tag of vertices
    private LinkedList<Integer> adjacency[];//adjacency list

    public AOVNetwork(int v) {
        V = v;
        adjacency = new LinkedList[v];
        for (int i = 0; i < v; i++) {
            adjacency[i] = new LinkedList<>();
        }
    }

    /**
     * add an edge from v to w
     * @param v
     * @param w
     */
    public void addEdge(int v, int w){
        adjacency[v].add(w);
    }

    /**
     * add edge from v to w1, w2, w3, ....
     * @param v
     * @param w
     */
    public void addEdges(int v, int... w){
        for (int ww : w) {
            adjacency[v].add(ww);
        }
    }

    @Override
    public String toString() {
        return "AOVNetwork{" +
                "V=" + V +
                ", adjacency=" + Arrays.toString(adjacency) +
                '}';
    }
}

topological sort

definition

摘抄自Wikipedia:

In the field of computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another

about partial order and total order

这是一个mathematic上的概念, partial order指的是: 在部分元素间的先后关系不确定的情况下而产生的排序, 如:

condition: x<=z, y<=z
result: x,y,z or y,x,z

而total order则是partial order的一个特例, 即: 在所有元素的先后关系都是完全确定的情况下而产生的排序, 如:

condition: x<=y, y<=z
result: x,y,z

如果topological sort是unique, 则说明该order是一个total order, 同时DAG存在hamiltonian path, 否则说明order是一个partial order

typical algorithms

解决topological sort的typical algorithms有两个:

  • Kahn’s algorithm
  • DFS

这两个algorithms的time complexity都是O(|V| + |E|), 由于DFS是一个十分强大和通用的algorithm, 为减小篇幅, 这里仅对Kahn’s algorithm进行介绍

Kahn’s algorithm

Kahn’s algorithm的伪代码:

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is non-empty do
    remove a node n from S
    add n to tail of L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least one cycle)
else 
    return L (a topologically sorted order)

the realization in java

public List<Integer> topologicalSorting(){
    LinkedList<Integer> sortedNodes = new LinkedList<>();//L, nodes that have bean sorted
    Set<Integer> zeroIndegreeNodes = new TreeSet<>();//S, nodes with no incoming edge

    LinkedList<Integer> transposeOfAdjacency[] = new LinkedList[V];//transpose of adjacency list

    //transpose of adjacency init
    IntStream.range(0, transposeOfAdjacency.length)
            .forEach(n -> {
                transposeOfAdjacency[n] = new LinkedList<>();
            });
    //tranform adjacency to transpose of adjacency
    IntStream.range(0, transposeOfAdjacency.length)
            .forEach(n -> {
                adjacency[n].stream().forEach(m ->{
                    transposeOfAdjacency[m].add(n);
                });
            });

    //zeroIndegreeNodes init
    IntStream.range(0, transposeOfAdjacency.length)
            .filter(i -> transposeOfAdjacency[i].size() == 0)
            .forEach(i -> {
                zeroIndegreeNodes.add(i);
            });
    //judge cycles
    if (zeroIndegreeNodes.isEmpty()){
        System.out.println("AOVNetwork has cycles");
        return null;
    }
    //Kahn's algorithm begin
    Iterator<Integer> iterator = zeroIndegreeNodes.iterator();
    while (iterator.hasNext()){
        Integer n = iterator.next();
        iterator.remove();//remove a node n from S

        sortedNodes.addLast(n);//add n to tail of L

        Iterator<Integer> mIterator = adjacency[n].iterator();
        while (mIterator.hasNext()){
            Integer m = mIterator.next();
            mIterator.remove();//remove edge e from the graph
            transposeOfAdjacency[m].remove(n);//remove edge e from the graph

            //judge does m has no other incoming edges
            if (transposeOfAdjacency[m].size() == 0){
                zeroIndegreeNodes.add(m);//insert m into S
            }
        }

        //reassign to iterator
        iterator = zeroIndegreeNodes.iterator();
    }

    //judge does graph has edges
    for (int i = 0; i < adjacency.length; i++) {
        if (adjacency[i].size() != 0){
            System.out.println("AOVNetwork has cycles");
            return null;
        }
    }

    return sortedNodes;
}

Kahn’s algorithm的示意图

Kahn_algorithm_1 Kahn_algorithm_2

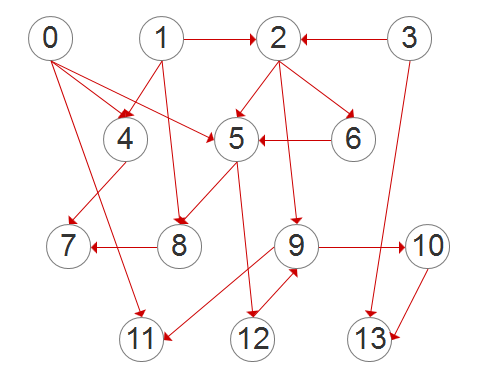
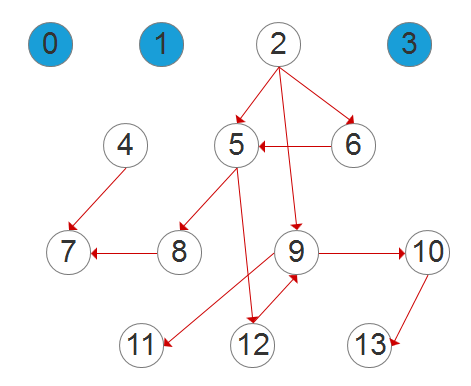
Conclusion: Kahn’s algorithm的实现十分简单明了, 仅需维护一个S集(Set of all nodes with no incoming edge)即可

references