The R2
about R2
这个toy完全是参照垠神这篇文章做的Java版翻译, 具体内容可以看垠神的文章, 下面是toy的一些细节和自己的总结
the basic match
(a b)–pattern–>ab–spilt–>E1: a E2: b(a (a b))–pattern–>a(a b)–spilt–>E1: a E2: (a b)((a b) b)–pattern–>(a b)b–spilt–>E1: (a b) E2: b((a b) (a b))–pattern–>(a b)(a b)–spilt–>E1: (a b) E2: (a b)
basic syntax and meaning
- 数字:
1 - 变量:
x - 函数:
(lambda (x) e)//执行e, 其中x是形参 - 绑定:
(let ([x e1]) e2)//执行e2, 而e2中x的值为e1, 常用与函数绑定 - 调用:
(e1 e2)//e1是函数符号, e2是函数入参 - 算术:
(@ e1 e2)//算式表达式
about env
the explain of env
在这个R2的解释器中, 环境的作用是保存所有出现过的变量所对应的值, 即所谓的变量作用域.
而文章中出现了两种不同的变量作用域, 分别是lexial scoping和dynamic scoping. 这两者最主要的区别静态和动态的区别. 如下例子:
(let ([x 2])
(let ([f (lambda (y) (* x y))])
(let ([x 4])
(f 3))))
;; => 12//dynamic scoping的结果
对于dynamic scoping, 由于变量的值是动态赋值的, 不存在前一个对x的赋值会影响到后一个对x的赋值, 也就是每次都是取变量x最新的值
(let ([x 2])
(let ([f (lambda (y) (* x y))])
(let ([x 4])
(f 3))))
;; => 6//lexical scoping的结果
对于lexical scoping, 变量x的值需要返回到定义这个变量的“环境”中取, 而这个特定的“环境”是在函数创建时确定的.
原因是函数只能“看到”创建时所对应的环境, 而创建后的环境是不在函数的范围内的. 所以, 取变量x的值需要返回函数“看到的环境”中取.
problems
但这里有两个问题, 一个是环境并存问题, 另一个是环境嵌套问题
考虑以下表达式
(+
(let ([x 2]) (let ([f, (lambda (y) (+ x y))]) (f 4))),
(let ([x 2]) (let ([f, (lambda (y) (* x y))]) (f 2))))
简单分析上述表达式, 可知有两个并存的环境, 如下图所示:
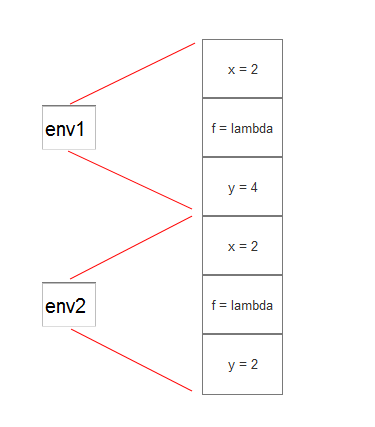
考虑以下表达式
(let ([x (let ([x 2])
(let ([f, (lambda (y) (+ x y))])
(f 3)))])
(let ([f (lambda (y) (* x y))])
(f 3)))
上述表达式是存在嵌套的环境的, 如下图所示:
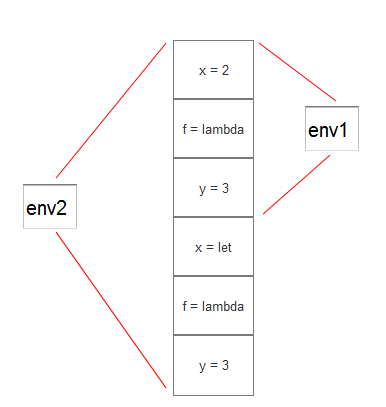
由于对lisp和闭包不熟悉, 所以也没有看出环境是否有实现上述两种结构, 而垠神的文章并没有给出相关的示例, 所以也不知道是否需要实现这种形式, 因此这两种形式的表达式都是无法解释的
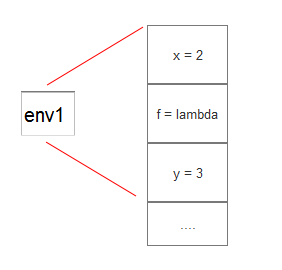
目前的代码只能解释最简单和普通的情况, 也就是只有一个特定的“环境”, 如下所示
(let ([x 2]) (let ([f, (lambda (y) (+ x y))]) (f 4))
reference
The Core Of Algorithm
what is algorithm
In my opinion, 算法实质就是描述某种抽象问题的解决方案. However, 这仅仅只是对那些比较高级和著名的算法而言, 如: DFS和BFS解决了如何遍历一个图, Shortest Path解决了节点间的最短路径问题.
而对于一般的算法, 它们应用的范围并不广泛, 用途仅仅只是解决某个特定问题, 如: 解决某一算法题所用到的算法. 这类算法通常是由最基本的操作所组成的
algorithm and math
algorithm和math的联系是非常紧密的, 而algorithm对应的数学分支是Concrete Mathematics. why? 下面用一个例子说明.
首先要明确的是, Concrete Mathematics是由集合论、图论、代数结构、组合数学和数理逻辑组成, 其中最为重要的是图论、代数结构和数理逻辑. 这三部分的知识是用得最多的, 下面也是围绕着这三部分进行讲解, 而这三部分的相关知识就不是这篇paper的讨论范围
对于一个实际的问题, 通过合理地建模, 便可运用相关知识进行分析
以下是建模的方式:
- 图论, 将现实中的结构化模型抽象成由点线组成的图
- 代数结构, 将输入看作是数据集, 而运算的过程中所涉及的所有操作看作是操作集
- 数理逻辑, 将整个运算过程转化成逻辑推理过程
basic operators
所有的algorithm都包含以下这些基本的操作, 这些操作在某种程度上是等同于基本运算法则, 如: 加减乘除、异或、同或. 而算法中最为常用的基本操作如下:
- 遍历(traverse)
//Pseudo code
for i = 1:n
...
end
- 交换(swap)
//Pseudo code
swap(a, b)
- 比较(comparation)
//Pseudo code
compare(a, b)
- 递归(recursion)
/**
* 写recursion的关键在于确定好边界条件
* 也就是退出递归的方式
* 不然会抛出SOE异常
*
* 下面以Fibonacci数列为例
* f(1) = 1
* f(2) = 2
* f(n+2) = f(n) + f(n+1)
* Pseudo code
*/
int f(n){
if(n == 1) return 1;
else if(n == 2) return 2;
else return f(n-1) + f(n-2);
}
下面以ISort为例, 近距离的观察算法是怎么运用到basic operators ISort的核心思想是假设序列中从0到k的元素是已排序的, 操作上通过将第k+1个元素与前K元素进行比较, 来确定第k+1个元素的在前k+1个元素的位置.
ISort的伪代码如下:
for i = 2:n,
for (k = i; k > 1 and a[k] < a[k-1]; k--)
swap a[k,k-1]
→ invariant: a[1..i] is sorted
end
下面分别用traverse和recursion来实现ISort
/**
* traverse版本
*/
void iSort(Integer[] a){
for (int i = 2; i < a.length; i++) {
for (int j = i; j > 0 && a[j] < a[j-1]; j--) {
a[j-1] = swap(a[j], a[j] = a[j-1]);
}
}
}
/**
* recursion版本
*/
void iSort2(Integer[] a, int index){
index++;
for (int j = index; j > 0 && a[j] < a[j-1]; j--) {
a[j-1] = swap(a[j], a[j] = a[j-1]);
}
if (index == a.length-1){
return;
}else {
iSort2(a, index);
}
}
important thought
在algorithm中, 有几个十分重要的思想,这些思想可以说是algorithm的核心,直接影响了一个具体algorithm的设计和实现
限于篇幅,下面仅仅只作提及,不进行详尽地描述, 如下:
- 贪心算法(gready algorithms)
- 分治策略(divide and conquer strategy)
- 动态规划(dynamic programming)
