about log framework

当前常用的log framework无非就是logback和log4j. 而由于log4j的可配置度低和功能较少, 所以实际上会用的比较少, 而更多的是使用logback作为log framework. Therefore, 这篇paper将写关于how to use logback.

basic concern

what is log

实质上, log是一个输出program各种信息的工具, 可以说存在于任何program中, 而不同的仅仅是其展示形式, 而常见的展示形式有: console out、file、数据库记录、页面弹出窗等等, 其中console out是最为常见的形式.

log level

log level可以说是log framework中最为重要的concern. why?

原因是log level如下作用:

1. 设置log level有助于区分log的类别和重要性, 并以此筛选有用的信息.
2. 通过控制log level来控制输出的log信息.
3. 由于输出了program的runtime信息, 所以对program的监控和调试都很有帮助.

log level可参考下图:

the form of log

log的形式实质上是可以多种多样的, 但运用logback最常使用的log形式有两种, 分别是:

• file log, 将log输出到指定的文件中
• console log, 将log输出到console中

about logback

关于logback的使用, 这里仅做简单的记录, 更详细的说明就参考这篇paper

如果要查看一个完整的logback配置实例, 则可参考这篇paper

logback configuration files

There are three valid standard file names you can choose from:

• logback-test.xml
• logback.groovy
• logback.xml

appenders

appenders are the elements responsible for writing log statements. All appenders must implement the Appender interface.

Furthermore, each appender corresponds to a certain type of output or mode of sending data. Here are some of the most helpful appenders you can configure:

• ConsoleAppender – writes messages to the system console
• FileAppender – appends messages to a file
• RollingFileAppender – extends the FileAppender with the ability to roll over log files
• SMTPAppender – sends log messages in an email, by default only for ERROR messages
• DBAppender – adds log events to a database
• SiftingAppender – separates logs based on a runtime attribute

上述是logback提供的appender, 实质上只需要实现Appender interface即可做custom appender, 示例如下:

• java code,
• xml配置:

<appender name="DEBUG-FILE-APPENDER" class="com.trasher.util.CountingFileAppender">
    <limit>100</limit>
    <file>${user.dir}/logs/debug.log</file>
    <encoder>
        <pattern>%date %level [%thread] %logger{10} [%file:%line] %msg%n
        </pattern>
    </encoder>
    <append>true</append>
</appender>

layouts and encoders

The components responsible for transforming a log message to the desired output format are layouts and encoders.

Layouts can only transform a message into String, while encoders are more flexible and can transform the message into a byte array, then write that to an OutputStream. This means encoders have more control over when and how bytes are written.

Some of the most commonly used layouts are PatternLayout, HTMLLayout and XMLLayout

loggers

Loggers are the third main component of Logback, which developers can use to log messages at a certain level.

configuration中的两种logger:

• root logger:

<root level="debug">
    <appender-ref ref="STDOUT" />
</root>

This sits at the top of the logger hierarchy and is provided by default, even if you don’t configure it explicitly, with a ConsoleAppender with the DEBUG level.

• normal logger.

<logger level="info" name="rollingFileLogger">
    <appender-ref ref="rollingFileAppender" />
</logger>

If you don’t explicitly define a log level, the logger will inherit the level of its closest ancestor; in this case, the DEBUG level of the root logger.

logger additivity

By default, a log message will be displayed by the logger which writes it, as well as the ancestor loggers. And, since root is the ancestor of all loggers, all messages will also be displayed by the root logger.

To disable this behavior, you need to set the additivity=false property on the logger element:

<logger level="info" name="rollingFileLogger" additivity=false>
   ...
</logger>

filtering logs

Logback has solid support for additional filtering, beyond just the log level, This is done with the help of filters – which determine whether a log message should be displayed or not.

三种不同的FilterReply:

• DENY. The DENY value indicates the log event will not be processed
• ACCEPT. ACCEPT means the log event is processed, skipping the evaluation of the remaining filters.
• NEUTRAL. NEUTRAL allows the next filters in the chain to be evaluated. If there are no more filters, the message is logged.

与log level有关的filter: LevelFilter和ThresholdFilter

对event做评估来决定是否输出log: GEventEvaluator和JaninoEventEvalutor

extending logback

For example, here are several ways you can extend Logback’s functionality:

• create a custom appender by extending the AppenderBase class and implementing the append() method
• create a custom layout by subclassing the LayoutBase class and defining a doLayout() method
• create a custom filter by extending the Filter class and implementing the decide() method
• create a custom TurboFilter by extending the TurboFilter class and overriding the decide() method

references

• https://stackify.com/logging-logback/
• https://www.mkyong.com/logging/logback-xml-example/
• https://logback.qos.ch/manual/introduction.html

activity on vertex network

the definition in logic

摘抄自某EDU:

definition A directed graph in which the vertices represent tasks or activities and the edges represent precedence relations between tasks.

To be careful: 在AOV中是不能有cycles, 让一个activity的开始要以自身的结束为条件, 这显然是不合理的, 即: Directed Acyclic Graph

the definition in mathematics

这个definition本质上就是DAG的definition

definition A graph G = (V,E), V and E are two sets, each edge is represented by a ordered pairs <u,v> V: finite non-empty set of vertices E: set of pairs of vertices, edges

Example: a graph G

• $$V(G) = {0, 1, 2, 3, 4}$$
• $$E(G) = {<0,1>,<0,3>,<1,2>,<3,1>,<3,2>}$$

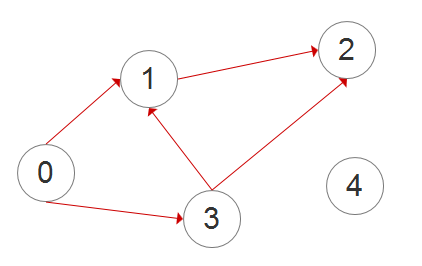
the realization in computer science

public class AOVNetwork {
    private int V;//no and tag of vertices
    private LinkedList<Integer> adjacency[];//adjacency list

    public AOVNetwork(int v) {
        V = v;
        adjacency = new LinkedList[v];
        for (int i = 0; i < v; i++) {
            adjacency[i] = new LinkedList<>();
        }
    }

    /**
     * add an edge from v to w
     * @param v
     * @param w
     */
    public void addEdge(int v, int w){
        adjacency[v].add(w);
    }

    /**
     * add edge from v to w1, w2, w3, ....
     * @param v
     * @param w
     */
    public void addEdges(int v, int... w){
        for (int ww : w) {
            adjacency[v].add(ww);
        }
    }

    @Override
    public String toString() {
        return "AOVNetwork{" +
                "V=" + V +
                ", adjacency=" + Arrays.toString(adjacency) +
                '}';
    }
}

topological sort

definition

摘抄自Wikipedia:

In the field of computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another

about partial order and total order

这是一个mathematic上的概念, partial order指的是: 在部分元素间的先后关系不确定的情况下而产生的排序, 如:

condition: x<=z, y<=z
result: x,y,z or y,x,z

而total order则是partial order的一个特例, 即: 在所有元素的先后关系都是完全确定的情况下而产生的排序, 如:

condition: x<=y, y<=z
result: x,y,z

如果topological sort是unique, 则说明该order是一个total order, 同时DAG存在hamiltonian path, 否则说明order是一个partial order

typical algorithms

解决topological sort的typical algorithms有两个:

• Kahn’s algorithm
• DFS

这两个algorithms的time complexity都是O(|V| + |E|), 由于DFS是一个十分强大和通用的algorithm, 为减小篇幅, 这里仅对Kahn’s algorithm进行介绍

Kahn’s algorithm

Kahn’s algorithm的伪代码:

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is non-empty do
    remove a node n from S
    add n to tail of L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least one cycle)
else 
    return L (a topologically sorted order)

the realization in java

public List<Integer> topologicalSorting(){
    LinkedList<Integer> sortedNodes = new LinkedList<>();//L, nodes that have bean sorted
    Set<Integer> zeroIndegreeNodes = new TreeSet<>();//S, nodes with no incoming edge

    LinkedList<Integer> transposeOfAdjacency[] = new LinkedList[V];//transpose of adjacency list

    //transpose of adjacency init
    IntStream.range(0, transposeOfAdjacency.length)
            .forEach(n -> {
                transposeOfAdjacency[n] = new LinkedList<>();
            });
    //tranform adjacency to transpose of adjacency
    IntStream.range(0, transposeOfAdjacency.length)
            .forEach(n -> {
                adjacency[n].stream().forEach(m ->{
                    transposeOfAdjacency[m].add(n);
                });
            });

    //zeroIndegreeNodes init
    IntStream.range(0, transposeOfAdjacency.length)
            .filter(i -> transposeOfAdjacency[i].size() == 0)
            .forEach(i -> {
                zeroIndegreeNodes.add(i);
            });
    //judge cycles
    if (zeroIndegreeNodes.isEmpty()){
        System.out.println("AOVNetwork has cycles");
        return null;
    }
    //Kahn's algorithm begin
    Iterator<Integer> iterator = zeroIndegreeNodes.iterator();
    while (iterator.hasNext()){
        Integer n = iterator.next();
        iterator.remove();//remove a node n from S

        sortedNodes.addLast(n);//add n to tail of L

        Iterator<Integer> mIterator = adjacency[n].iterator();
        while (mIterator.hasNext()){
            Integer m = mIterator.next();
            mIterator.remove();//remove edge e from the graph
            transposeOfAdjacency[m].remove(n);//remove edge e from the graph

            //judge does m has no other incoming edges
            if (transposeOfAdjacency[m].size() == 0){
                zeroIndegreeNodes.add(m);//insert m into S
            }
        }

        //reassign to iterator
        iterator = zeroIndegreeNodes.iterator();
    }

    //judge does graph has edges
    for (int i = 0; i < adjacency.length; i++) {
        if (adjacency[i].size() != 0){
            System.out.println("AOVNetwork has cycles");
            return null;
        }
    }

    return sortedNodes;
}

Kahn’s algorithm的示意图

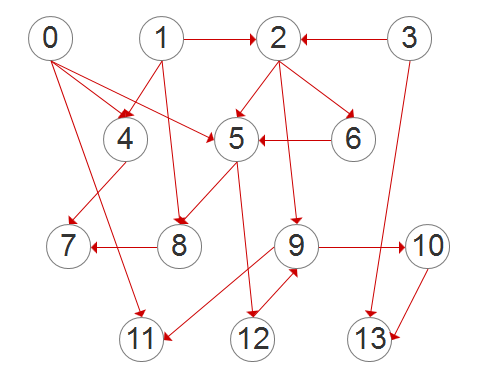
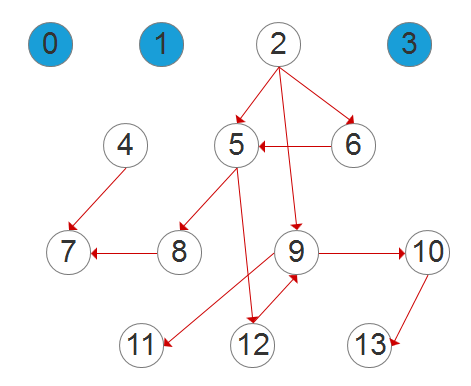
Conclusion: Kahn’s algorithm的实现十分简单明了, 仅需维护一个S集(Set of all nodes with no incoming edge)即可

references

• https://www.geeksforgeeks.org/topological-sorting/
• https://www.csie.ntu.edu.tw/~ds/ppt/ch6/sld080.htm
• http://blog.csdn.net/dm_vincent/article/details/7714519
• http://en.wikipedia.org/wiki/Topological_sorting
• http://en.wikipedia.org/wiki/Hamiltonian_path
• http://blog.csdn.net/jnu_simba/article/details/8872847
• http://www.nhu.edu.tw/~chun/DS(I)-Ch06-Graphs.pdf